通过获取金属材料层错能大小,快速了解材料的基本性能。
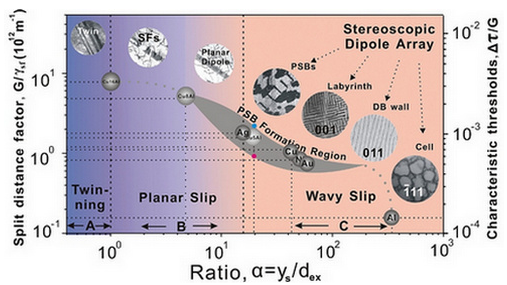
随着现代工业的迅速发展,工业界对于具有高强度、高塑性、高疲劳性能的金属材料具有重要的需求。层错能对材料的微观结构、拉伸性能、强韧化机制以及疲劳行为等方面有着重大影响。因而,层错能大小对高氮钢、TWIP钢及镍钴基高温合金等工程材料的变形机制、强韧化与抗疲劳设计具有重要指导意义。 曾经,层错能被视为区分滑移方式的首要因素,但除层错能外,滑移方式还受到短程有序、晶格摩擦应力、外加载荷等内外因素影响。因此,通过将螺位错湮灭距离与扩展位错宽度的比值作为因子来研究位错组态演化。 研究表明,演化因子越高,层错宽度变窄而湮灭距离增大,晶体材料将以典型波状滑移方式为主,交滑移频繁发生,进而基于取向效应形成越低;层错宽度增加而湮灭距离缩小,交滑移越困难,材料以平面滑移方式为主,因此更易出现二维平面位错结构。 正是由于不同面心立方金属具有不同的演化因子,因而其塑性变形与疲劳损伤过程中位错演化表现出截然不同的规律。
中国科学院金属研究所材料以Cu和Cu合金(Cu-Al,Cu-Zn等)模型材料研究了层错能对微观结构、拉伸性能、强韧化机制以及疲劳行为等方面的影响规律。 研究表明在铜中加入合金元素能降低层错能,改变位错滑移方式,乃至引入层错与孪晶,不但可以有效提高屈服强度,而且在很大程度上可以提高加工硬化能力与均匀延伸率 ,从而实现强度与塑性同步提升的效果。
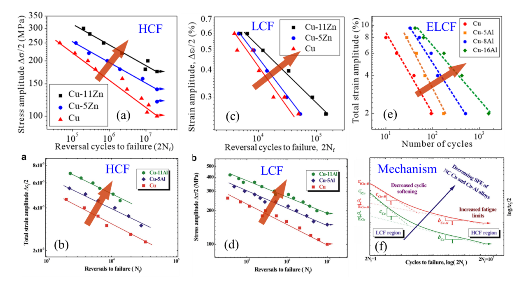
这种通过降低层错能改善加工硬化能力的原因可以归纳为: 1)增加位错平面滑移程度,降低位错交滑移倾向性及湮灭距离,从而实现更高位错密度的存储,增加加工硬化能力。 2)增加层错及孪晶的萌生能力,促使塑性变形过程中层错与变形孪晶的出现,将常见于钢中的孪生诱发塑性(TWIP)机制及动态Hall-Petch效应引入铜合金中,增加加工硬化能力。 此外,随着层错能降低,不但强度与塑性同步提升,而且铜合金的疲劳寿命也会同步提升 ,即随着合金元素含量增加或层错能降低,无论是铜铝合金还是铜锌合金,其高周、低周及超低周疲劳寿命均得到明显提高。
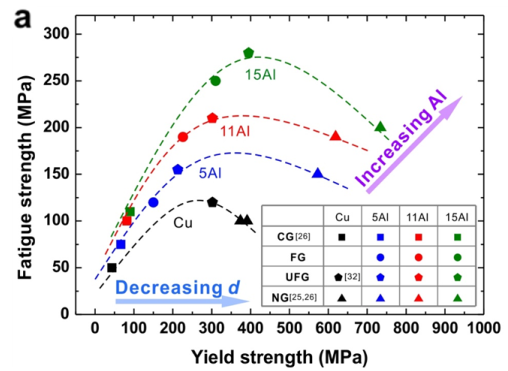
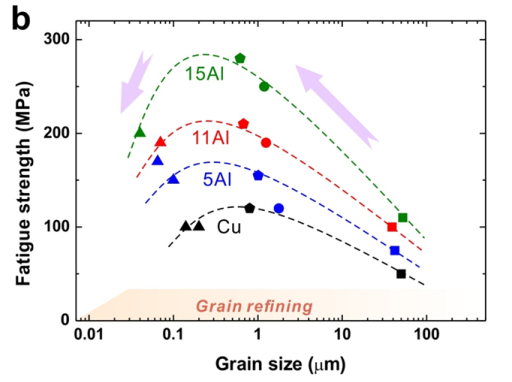
层错能对超细晶纳米晶材料疲劳损伤机制的影响可以理解为: 1)随着层错能降低,位错交滑移能力下降,从而减缓了因交滑移而导致的位错湮灭。而这将阻碍由疲劳而引起的晶界迁移、晶界滑移以及晶界转动,因而材料的组织稳定性得到了改善,循环软化行为也得到了减缓。 2)层错能的降低也有利于延缓材料疲劳后表面剪切带的演化,从而抑制了组织在变形过程中发生的应变局部化,增加了变形均匀程度。这两者都有利于抑制材料循环软化,延长材料的疲劳寿命。 然而,近期研究证实,对于特定成分材料,当大范围调整其晶粒尺寸来改变强度时,材料的疲劳强度随抗拉强度增加先升高然后再降低,即具有高强度的纳米晶金属材料的疲劳强度不是最优状态。 材料强化初期,抗拉强度提高降低了循环变形过程中局部塑性屈服的概率与程度,减缓了疲劳损伤,因而提升了疲劳性能,因此表现出疲劳强度随抗拉强度增加而升高;而在强化后期,因基体硬化能力过度缺失而引起基体对缺陷的敏感程度急剧增加反而增加了疲劳损伤程度,因而造成疲劳强度随抗拉强度提高而降低。这种先升后降的规律使得材料强化对疲劳性能的贡献大打折扣。 随着材料层错能降低,由于形变均匀性提高使疲劳损伤程度整体减弱,因而这种疲劳强度随抗拉强度提高或晶粒尺寸减小而表现出的先升后降的趋势在很大程度上被推迟。 因此,临界晶粒尺寸(疲劳强度取得极值时的晶粒尺寸)随层错能降低而减小,对应临界抗拉强度相应增加,最终促使疲劳强度得到大幅度提升 。
那么,有人可能要问了,既然层错能对材料性能那么重要,如何才能快速计算出金属材料的层错能呢? 目前,层错能的计算方法有很多种,主要包括有热力学计算、透射电镜层错宽度测量法、XRD峰值法等。其中,热力学计算方法由于比较成熟,有效得到广泛应用。 但是,热力学计算层错能需要统计各类热力学参数。因此,想快速得出层错能来了解材料性能就比较困难了。 为了解决这一问题,我们开发了一款免费且简便好用的小工具, 希望能对你的研究和写作有所帮助。
它简单易用 ,进入网站 (点击本公众号“Goal Science”栏目,科研资源→层错能计算)计 算 层错能
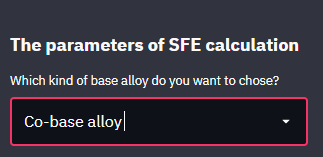
下面我们以Co-10Ni-5Mo-0.1Si合金为例来计算合金的层错能大小。 这里,我们首先输入想要计算的合金类型,主要有钴基、镍基与铁基三类。我们选择钴基合金。
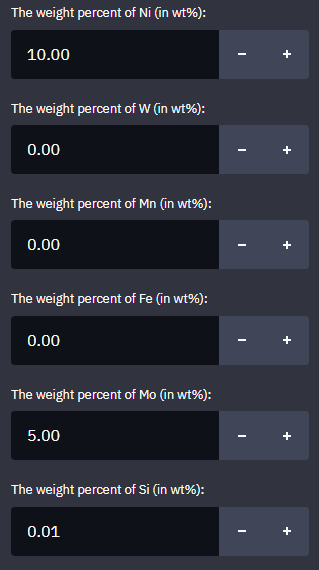
然后输入各元素重量百分比。
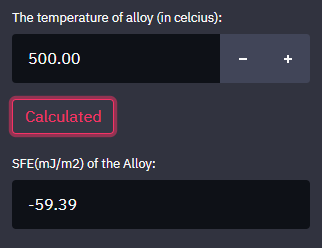
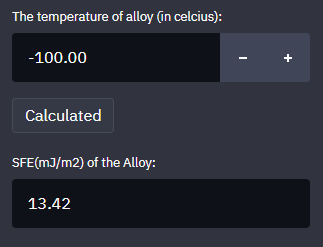
输入温度500℃后,点击Calculated。
那么,最终我们得到Co-10Ni-5Mo-0.1Si合金在500℃下的层错能为-59.39mJ/m2。 我们推出的这款app计算方法原理及数据来自发表在JAC上的一篇科学研究论文,文中对层错能的计算原理及方法有详尽的叙述,感兴趣的可以下载原文进行查看。
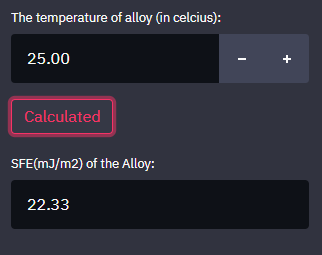
我们以最近在Scripta上发表的Temperature dependent deformation behavior and stacking fault energy of Fe40Mn40Co10Cr10 alloy一文中的Fe40Mn40Co10Cr10合金为例,在室温(RT)和-100℃下计算的SFE分别为22.33mJ/m2和13.42mJ/m2,
与文中利用透射电镜弱束暗场的实验计算方法的结果(分别为37.7(±7)mJ/m2和19.5(±5)mJ/m2)较为一致,看来准确性还可以。 同时,我们可以对各种不同合金元素进行参数设定。
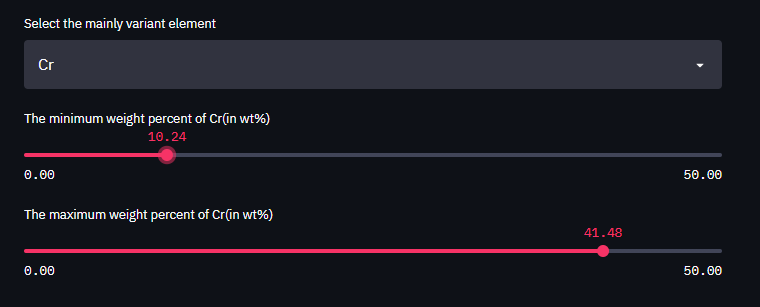
例如选择变量元素为Cr,调节其含量为10.24%~41.48%。
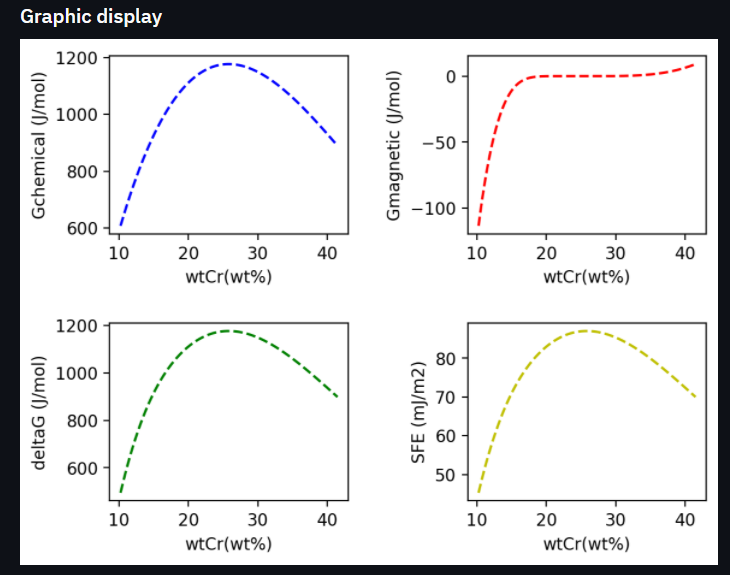
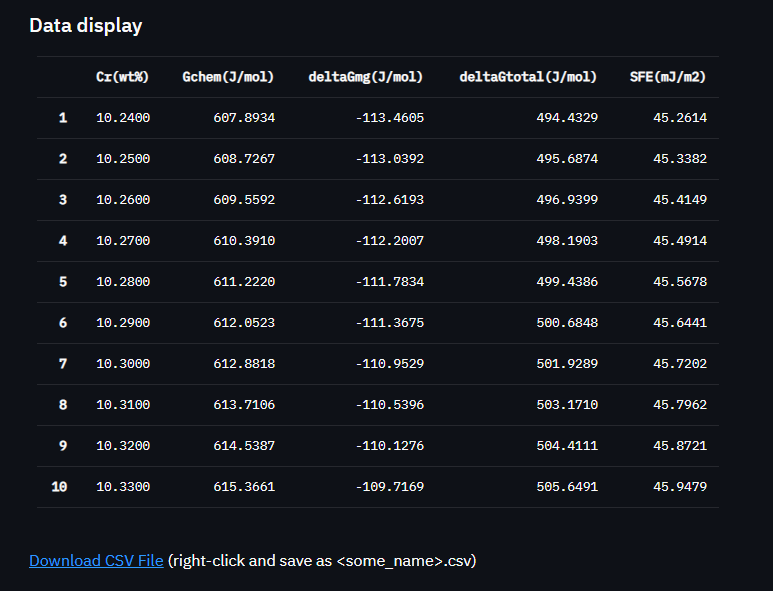
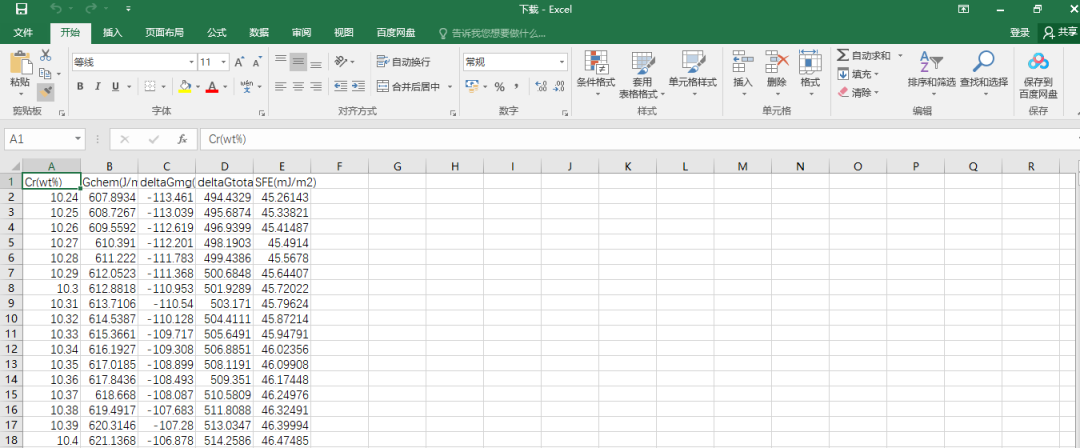
其中,Gchemical为化学自由能变化值,Gmagnetic为磁性能的变化值,deltaG为吉布斯自由能的变化,最后是SFE层错能随Cr含量的变化。 计算结果的前10行数据会进行展示。当然,我们也可以点击Download CSV File 将计算结果进行导出,
自动转换结果为 CSV ,然后用 Excel 打开。
我们发现,数据形式都比较标准,可以直接做分析用。当然,如果有打不开csv文件的,可以用记事本打开,或者使用notepad++编译器打开。 如果你想具体了解层错能的计算方法,或想将计算的数据用作论文写作材料,可以引用以下论文,
最后,如果你对层错能的计算或使用上有好的想法或建议,欢迎进行反馈与交流。
读完这篇文章后,相信你对层错能的计算有了进一步的了解:
层错能对高氮钢、TWIP钢及镍钴基高温合金等工程材料的变形机制、强韧化与抗疲劳设计 具有重要指导意义;
能够快速计算不同种类合金的层错能大小 ,以及合金层错能随元素的变化情况趋势;
将计算结果导出为可读的 CSV 格式 进行数据分析。
参考文章:
面心立方金属层错能效应研究取得新进展